SUBMENU

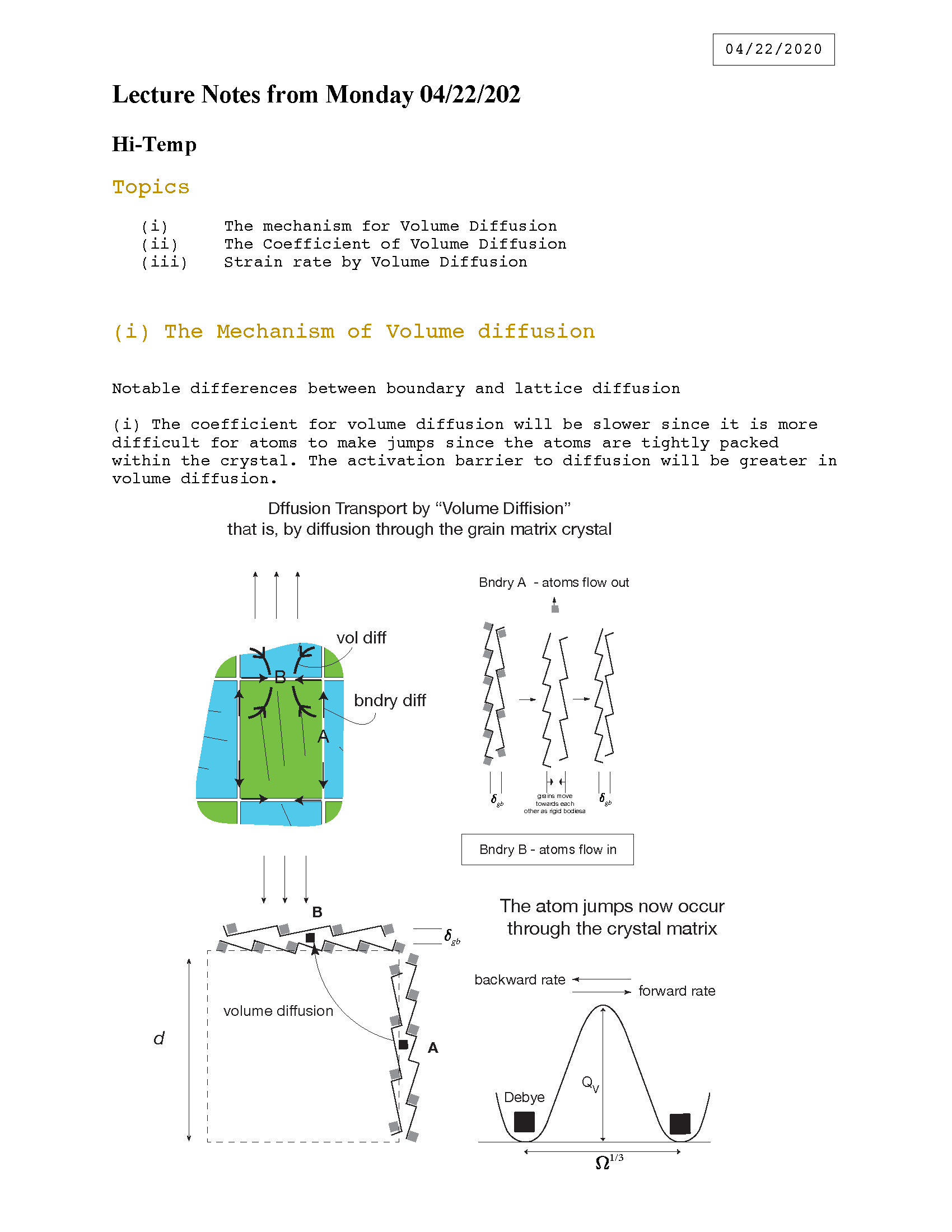
Topic IV - Deformation by Solid State Diffusion at High Temperature
New
HW Exam IV
Assigned Monday 04/27/20, due Monday 05/04/20
Take Home Exam IV - Hi TempIntroduction
It is quite remarkable that very large deformations, so called superplasticity, is possible by such atom-wise transport of mass, as illustrated by the figure just below
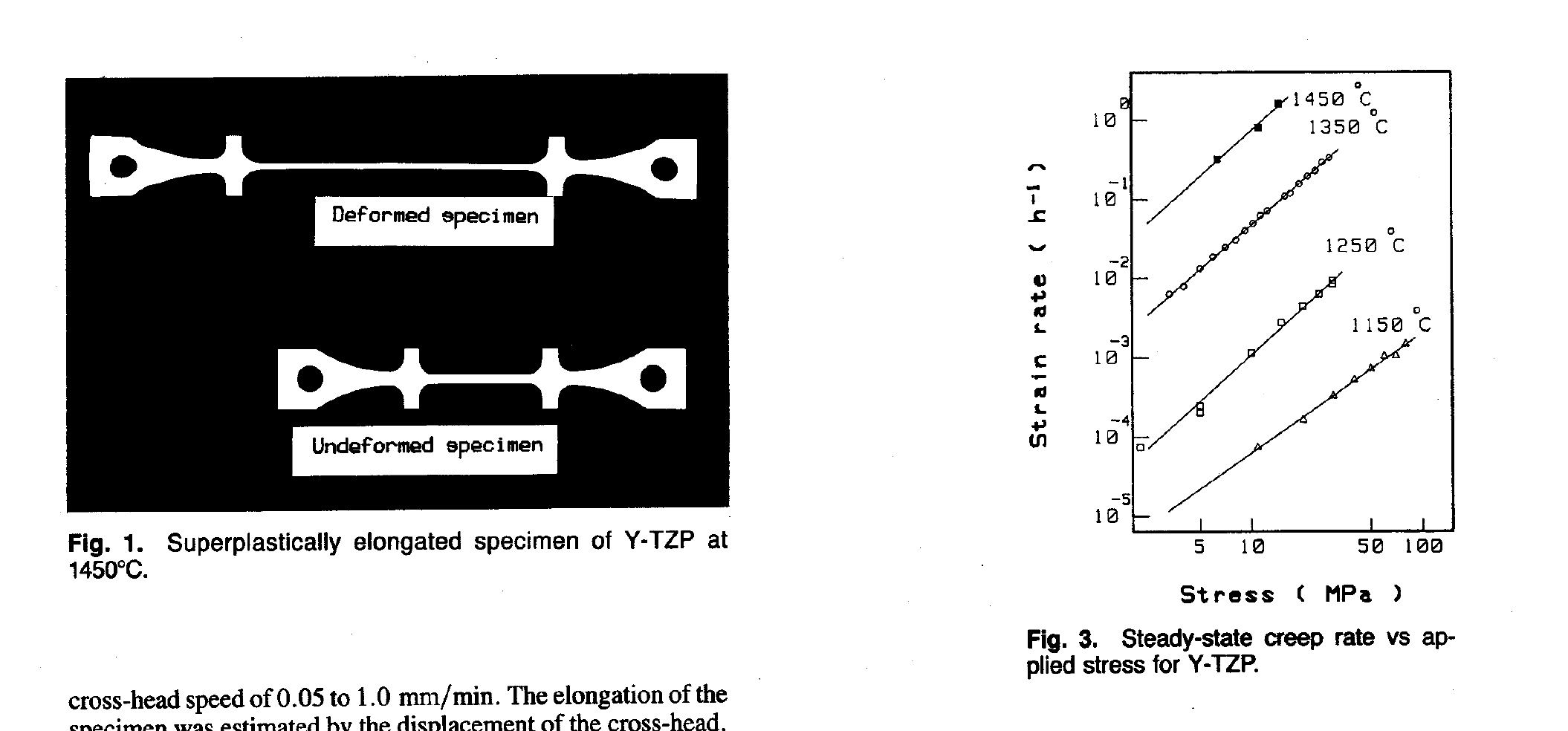
which is from this paper: Wakai in the late Eighties
Strain Induced by Atom-by-Atom Transport of Mass Between Grain Boundaries
The notes from this class are bundled together in the following pdf file




Strain Rate from Grain Boundary Diffusion
The notes from this class are bundled together in the following pdf file








Strain Rate from "Volume" Diffusion
The notes from this class are bundled together in the following pdf file